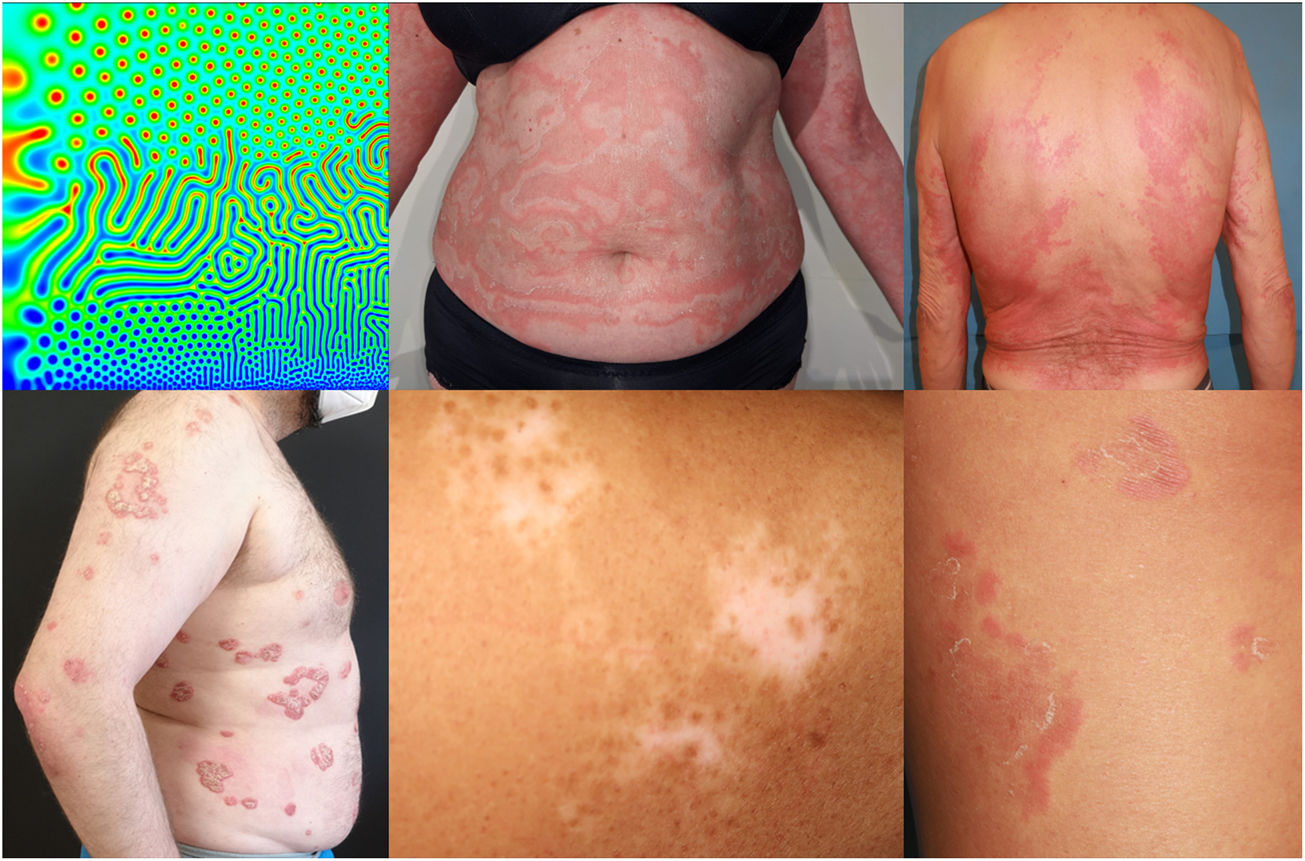
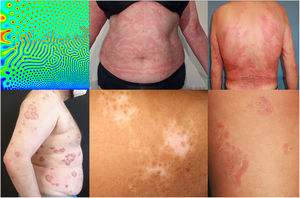
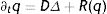Reaction–diffusion systems were described by Alan Turing in his 1952 article entitled “The chemical basis of morphogenesis.” The mathematical model he proposed explains how different complex patterns can emerge. It is based on 2 or more substances, denoted morphogens, which diffuse through a continuous medium and interact with each other. According to the type of interaction, different patterns form stochastically. The interactions can be represented in simplified form using the following formula:
where each component of the vector q(x,t) represents the concentration of a substance, D is the diagonal matrix of diffusion coefficients, Δ denotes the Laplace operator, and R represents local reactions (Fig. 1).According to the different dynamics of the resulting reactions and their wavelength, there are 6 distinct different potential states. In the fourth case, also known as the Turing pattern, a nonlinear wave is formed in dynamic equilibrium, the wavelength of which is determined by the interactions between substances and their diffusion rates. These Turing patterns emerge independently and tend to regenerate by themselves following perturbations.1
Turing patterns combine positive and negative feedback systems. An almost infinite number of patterns can be formed as the quantity and type of substances vary. Substances can be simple entities such as molecules, or complex, like cell signaling pathways. Furthermore, they adjust to diffusion in different media as phenomena of chemiotaxis and action potentials.
The distribution of feathers on birds, embryonic development of limbs, and the bronchial tree are examples of Turing patterns in nature.2 The characteristics of Turing patterns are more evident in 2-dimensional models such as the skin. Examples include the pattern of spots on leopards and the stripes on cebras.2
Turing patterns have only recently found an application in dermatology. Morphogenesis of hair follicles can be explained by Turing patterns, in which interaction of BMP (bone morphogenic protein), FGF (fibroblast growth factor), and WNT (wingless protein) cell signaling pathways give rise to the epidermal and dermal condensate from which the papilla originates.3 The different morphological patterns of chronic spontaneous urticaria (CSU) can be explained by the activation/inhibition model of histamine.4 The morphology and rate of appearance of wheals in CSU is different to those produced by intradermal histamine reaction. In CSU, the rate of wheal formation is slower, they last longer, and they can acquire annular or arciform patterns, in contrast to the circular wheals of intradermal reaction.4 The morphological patterns of psoriasis (annular, circinate, rosacea, large plaques) and evolution can also be explained by Turing patterns and the interaction between pathogenic cytokines tumor necrosis factor, interleukin (IL) 17, and IL-23.5
Mathematical models such as Turing patterns can explain the phenotype of different skin diseases. The role of the dermatologist is essential in the search for different molecules, cell signaling pathways, and their interactions, which can explain these processes.
FundingThis article did not receive any funding.