INTRODUCCION

La Dermatología, como el resto de la medicina, está sufriendo una revolución sin precedentes y debe posicionarse en este mundo cambiante. La Dermatología no puede ignorar ahora la investigación clínica, la medicina basada en la evidencia y la epidemiología, sin olvidar la dermatología clínica, la dermatopatología, la dermatocirugía, las dermatociencias y la dermatología basada en la apariencia1.

Los estudios epidemiológicos se dividen en dos grupos según sus objetivos. El primero reúne aquellos estudios dirigidos a determinar la frecuencia de enfermedad en una población. El otro grupo está compuesto por los que tienen como finalidad evaluar la asociación entre exposición y frecuencia de la enfermedad. En esta revisión expondremos los conocimientos que permiten realizar y/o comprender el primer grupo de estudios y describiremos el segundo tipo de estudios con los errores que con más frecuencia pueden presentar.

Esto permite, con un cierto conocimiento de los métodos de investigación y sin necesidad de grandes fórmulas matemáticas, juzgar por uno mismo la validez de lo que otros publican y su posible aplicación en nuestros pacientes. La precisión y la validez interna son indicadores de la calidad de cualquier diseño. Estudios poco precisos y/o con poca validez interna no tienen mayor interés en cuanto a la validez externa, y no aportan nada, aparte de un punto más en el currículum vitae del autor.

Para realizar una buena investigación clínica, el clínico debe buscar ayuda metodológica mucho antes de empezar el estudio, y sólo analizar datos de cuya validez interna está convencido.

Por otra parte, para evaluar la calidad de la investigación clínica que se publica en España, y secundariamente el grado de interacción existente entre medicina clínica y epidemiología es necesario conocer los diferentes tipos de estudios; así, podemos observar que la mayoría de los artículos publicados son diseños sin posibilidades inferenciales (comunicaciones de casos y series clínicas), hecho que pone de manifiesto cierta falta de competitividad internacional de la producción científica española2.

En esta monografía no se ha realizado una búsqueda de estudios con errores de diseño al existir ya un «bestiario» con errores metodológicos en estudios epidemiológicos que todo lector crítico debe conocer3.

¿QUÉ ES LA EPIDEMIOLOGIA?

La epidemiología es la ciencia que estudia la frecuencia de las enfermedades en las poblaciones humanas. Consiste en la medición de la frecuencia de la enfermedad y en el análisis de sus relaciones con diversas características de los individuos o de su medio ambiente4. La palabra epidemiología proviene de los términos griegos, «epi» = sobre, encima, «demos» = pueblo y «logos» = estudio y significa el estudio de lo que está sobre, o que afecta a las personas. Sin embargo, el desarrollo de la teoría y métodos epidemiológicos en las últimas décadas ha abierto nuevas perspectivas y despertado gran interés en múltiples campos de aplicación.

La mayoría de los trabajos de investigación realizan comparaciones entre dos o más grupos de enfermos, o entre enfermos e individuos sanos en un mismo estudio o bien con otros estudios de otros investigadores. Para poder realizar estas comparaciones disponemos de diferentes medidas de frecuencia, y para poder comparar las frecuencias en ambos grupos debemos utilizar el mismo tipo de medida. Muchas veces las medidas de frecuencia se utilizan equivocadamente como adjetivos que se aplican a números que quieren expresar frecuencia, especialmente común es la confusión entre tasa y proporción4,5.

Proporciones y razones

La frecuencia de un suceso clínico puede medirse de cuatro formas simples: con un número, con una proporción, con una razón y con una tasa.

Con un número: por ejemplo, decimos que en junio hemos visto 12 casos nuevos de psoriasis.

Con una proporción: el numerador está incluido en el denominador. Por ejemplo, decimos que de 400 pacientes atendidos en nuestra consulta 12 tenían psoriasis. La proporción es 12/400 = 0,03. Muchas veces la proporción se expresa en porcentaje, multiplicando por 100. En nuestro caso decimos que el 3 % de los pacientes atendidos en nuestra consulta en junio tenían psoriasis.

Con una razón: usamos un quebrado cuyo denominador no contiene al numerador. Por ejemplo: entre los afectados de lupus eritematoso sistémico, la razón mujeres/varones es de 13:1.

Con una tasa: es una forma especial de proporción que tiene en cuenta el tiempo: el numerador está incluido en el denominador y éste incluye una unidad de tiempo. Por ejemplo la expresión «la tasa anual de nuevos casos de cáncer cutáneo entre hombres de 60 a 70 años es de 12 por cada 1.000 personas de riesgo» se refiere a que por cada aumento en la unidad de tiempo (1 año) la tasa de cambio desde la situación clínica de no enfermo a la de enfermo, en aquellas personas con riesgo de contraer la enfermedad (hombres de 60 a 70 años) es de 12 casos por cada 1.000 personas. La dimensión temporal a la que se refieren las tasas no es un período delimitado entre dos puntos temporales, sino que las tasas son medidas instantáneas del cambio de valor de una variable por cada unidad de otra variable de la cual depende la primera. Para explicar intuitivamente el concepto de tasa, puede utilizarse una tasa de uso común, la velocidad en el automóvil en un instante dado es una tasa que se expresa como km/h, viajar a 100 km/h no significa que hayamos recorrido 100 km en una hora, ni que necesariamente vayamos a recorrerlos. De hecho, podemos ir a 100 km/h sin estar toda una hora montados en el coche. Del mismo modo, en el ejemplo anterior sobre el cáncer cutáneo, la tasa no expresa el número de casos nuevos en 1 año, sino la velocidad con que se produce el cambio de una situación clínica (sano) a otra (enfermo) en una población determinada4-10.

MEDIDAS DE FRECUENCIA DE ENFERMEDAD

El objetivo inicial de los estudios epidemiológicos es el conocimiento de la frecuencia de la enfermedad. Las medidas de frecuencia de enfermedad pueden ser expresadas de distintas maneras.

Valores absolutos y valores relativos

Las medidas de frecuencia de enfermedad deben ser independientes del tamaño de la población. Esto se consigue relacionando el número de casos de enfermedad que surgen en una población con el número de individuos de la misma. La información sobre el número de casos puede ser suficiente para la realización de tareas administrativas, pero el análisis epidemiológico requiere la consideración del tamaño de la población.

Por ejemplo: Ciertos datos epidemiológicos se utilizaron en una campaña de promoción del uso de fotoprotectores. De entre 222 pacientes con cáncer cutáneo, solamente 16 usaban fotoprotectores. Estos datos parecían sugerir la existencia de una relación entre el no uso de fotoprotectores y el riesgo de cáncer cutáneo. Sin embargo la comparación así establecida entre las cantidades absolutas de casos ignora la frecuencia de uso de fotoprotectores, es decir, el tamaño de la población que lo utiliza y el de la que no lo usa. Por ello la diferencia anteriormente aludida podría reflejar únicamente el hecho de que el número de usuarios de fotoprotectores es habitualmente pequeño en comparación con el de los que no lo aplican.

Incidencia y prevalencia

Las medidas de frecuencia de enfermedad pueden referirse al conjunto de casos existentes o a la aparición de casos nuevos. Las medidas de prevalencia describen la proporción de la población que padece la enfermedad en estudio en un momento dado. Las medidas de incidencia se refieren al número de casos nuevos que aparecen en un período de tiempo. La prevalencia depende obviamente de la incidencia, pero también de la duración de la enfermedad. Esto significa que las modificaciones de la prevalencia pueden deberse a variaciones en la incidencia o bien a cambios en la duración de la enfermedad. Las variaciones en la duración de la enfermedad pueden a su vez depender de cambios en el período de recuperación o en la esperanza de vida de los pacientes11,12.

Tres medidas de frecuencia de enfermedad

Prevalencia. La medida de prevalencia se denomina únicamente «prevalencia» (P) y se define como:

P = N.º de individuos que tienen la enfermedad en un momento dado/

N.º de individuos de la población en ese momento

La prevalencia es la proporción de la población que padece la enfermedad en un momento dado. Como todas las proporciones, no tiene dimensiones y nunca puede tomar valores menores de 0 ni mayores de 1.

Incidencia acumulada. La llamada «incidencia acumulada» (IA) se define como:

IA = N.º de individuos que presentan la enfermedad durante un período de tiempo determinado/

N.º de individuos de la población al comienzo de ese período

La incidencia acumulada es la proporción de individuos sanos al comienzo del período que pasan durante el mismo al estado de enfermedad. Es decir, el numerador es un subgrupo del denominador. La incidencia acumulada es una proporción, sus valores numéricos sólo pueden variar entre 0 y 1.

Tasa de incidencia. La medida fundamental de frecuencia de enfermedad es la tasa de incidencia (I), también denominada densidad de incidencia, que se define como:

I = N.º de casos de la enfermedad que aparecen en una población durante un período de tiempo determinado/

Suma de los períodos de tiempo en riesgo de contraer la enfermedad correspondientes a cada individuo de la población

¿Qué medida de frecuencia usar? En un estudio clínico, la elección de una determinada medida de la frecuencia depende primordialmente de la hipótesis de trabajo5. Se elige la incidencia si el objetivo es examinar una relación causal o evaluar una intervención médica (preventiva o terapéutica), ya que los casos incidentes son los que ocurren debido a ese hipotético factor de riesgo o a la actuación médica. Si se puede realizar un seguimiento de cada individuo incluido en el estudio, se incorpora el tiempo de observación, construyendo las tasas de incidencia, esto es preferible al simple uso de proporciones. Si nuestro estudio es descriptivo, la elección de la medida dependerá del período de latencia o de incubación y de la duración de la enfermedad. La elección entre incidencia y prevalencia a menudo se hace desde un punto de vista pragmático. En general, en los estudios epidemiológicos de enfermedades crónicas, como la psoriasis, se utilizan medidas de prevalencia, mientras que en los referidos a otras enfermedades como el cáncer se suelen emplear medidas de incidencia12.

Por ejemplo: La prevalencia de la psoriasis (u otra enfermedad de curso prolongado) describe mejor el problema sanitario que supone esta enfermedad que la incidencia. En cambio, para estimar la frecuencia del impétigo (u otra enfermedad de curso breve) es preferible usar la incidencia ya que dada la corta duración de los casos, la prevalencia nos daría una idea bastante pobre de su importancia sanitaria.

Medidas crudas y específicas. Las medidas de frecuencia de enfermedad pueden ser calculadas para una población o, por separado, para grupos de la misma. En el primer caso las medidas se denominan crudas y en el segundo específicas. Por ejemplo, si las tasas de incidencia se calculan para diferentes grupos de edad de una población, serán denominadas tasas de incidencia específica por edad. Cuando existe una razón para pensar que la frecuencia de la enfermedad puede variar de un grupo a otro se divide la población en subgrupos. Estas variaciones pueden tener interés y permanecen ocultas si sólo se obtuviesen las medidas crudas. Otra razón importante en las comparaciones entre poblaciones, es que la magnitud de la medida cruda no depende sólo de la magnitud de las medidas específicas que se aplican a los subgrupos, sino también de la forma en que la población se distribuye en diferentes poblaciones4,6,7.

Por ejemplo: durante el año 2000 la tasa cruda de incidencia de cáncer cutáneo en el área V de Salud (Gijón) del Principado de Asturias fue de 250 por 100.000 habitantes, mientras que en el área VI (Arriondas) fue de 315 por 100.000 habitantes. La explicación de esta diferencia no es que el riesgo de padecer cáncer cutáneo fuese mayor en el área VI que en el área V. Todas las tasas específicas por edad fueron mayores en el área V que en el área VI. La explicación es que los grupos de edad avanzada, donde la incidencia del cáncer cutáneo por edad es más alta, constituyen una mayor proporción de la población en el área VI que en el área V13.

MEDIDAS DE FRECUENCIA COMPARADA DE ENFERMEDAD

Una vez valoradas y conocidas las tasas (de incidencia, de prevalencia, de mortalidad, letalidad, etc.) se plantea el problema de comparación entre nuestros datos y los datos obtenidos en otros estudios. La pregunta es: ¿es mi tasa mayor, igual o menor que la encontrada en otros estudios?

Para comprobar esta pregunta es necesario realizar una estandarización que permita realizar la comparación. La estandarización se puede realizar por el método directo e indirecto.

Procedimiento de resolución

A. Método directo14,15

1. Calcular la tasa específica (o bruta) para la población estudiada.

2. Distribuir por grupos de edad la población estudiada y conocer cuántos habitantes están distribuidos por grupo de edad.

3. Conocidos estos elementos proceder a obtener la tasa específica por grupos de edad.

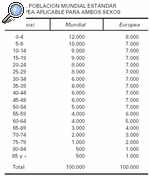
4. Con las tasas por grupo de edad, calcular cuántos casos se esperarían en una población ideal (habitualmente se utiliza la población mundial modificada de Seguí, o la población estándar europea) (tabla 1).

5. Sumar todos los casos hallados en el punto anterior para cada grupo de edad, de esa manera tendremos los casos totales.

6. Dividir los casos totales en el número de habitantes de la población ideal.

7. La tasa obtenida x 1.000 es la tasa ajustada.

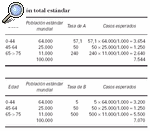
En el ejemplo se muestran dos poblaciones cuyas frecuencias de carcinoma basocelular se intentan comparar. Esta comparación podría realizarse utilizando las dos tasas crudas de incidencia, 100 por 1.000 en la población A y 101,9 por 1.000 en la población B. Sin embargo, este procedimiento no sería correcto debido a que la distribución por edad de las poblaciones es diferente. Al realizar la estandarización por el método directo se puede observar que, a pesar de que la población B presenta una tasa de incidencia bruta más elevada, tiene una menor tasa estandarizada porque tiene una mayor proporción de personas de edad avanzada. En este caso, la distribución por edades podría explicar que esta población tenga una tasa cruda de incidencia mayor.

Ejemplo: pasos 1, 2, 3

Pasos 4, 5. Se calcula mediante la siguiente fórmula:

Sumatorio (tasa parcial por grupo de edad x población del grupo de edad en la población estándar

Pasos 6, 7:

Tasa ajustada de A = (7.544/100.000) x 1.000 = 75,4 x 1.000

Tasa ajustada de B = (707/100.000) x 1.000 = 70,7 x 1.000

Un problema del ajuste de tasas es la elección de la población estándar. En principio, la población estándar debe reflejar la distribución de la población a la que se refieren las medidas del efecto estimadas, pero con frecuencia su significado no está claro. Si en el ejemplo anterior se hubiera elegido otra población estándar, por ejemplo la población estándar europea, la razón de tasas ajustadas obtenida hubiese sido distinta. Éste es el motivo que nos impide la comparación directa de los artículos europeos con la mayoría de los artículos norteamericanos que utilizan la población blanca de EE.UU. 199016, o la población canadiense17.

Para poder realizar las comparaciones en los artículos debe figurar la población estándar utilizada como referencia, y estandarizar nuestros datos por la población utilizada en los artículos con los que lo queremos comparar18,19.

B. Método indirecto

El ejemplo siguiente describe una situación bastante frecuente. La información acerca de las dos poblaciones que en ella se expone es la misma que la del ejemplo anterior, excepto que no se dispone del número de casos específico para cada grupo de edad en la población expuesta. Un motivo frecuente de esta falta de información es que el número de casos fuera tan pequeño que su reparto entre los grupos de edad pudiera ser inapropiado.

La comparación en estas situaciones se establece entre el número de casos observados en la población expuesta y el correspondiente número de casos «esperados». El número de casos observados en el ejemplo es de 50. Los casos «esperados» son aquellos que hubiesen aparecido en la población A, si ambas poblaciones, A y B, hubieran presentado las mismas tasas de incidencia específica por edad. En este ejemplo el número de casos esperados sería:

(175 x 5) + (200 x 50) + (125 x 500)/1.000 = 73,35

Tanto el número de casos observados como el de esperados se obtienen de una población cuya composición por edades es la de la población expuesta. Sin embargo, las tasas de incidencia sobre las que se calculan los casos esperados son las de la población de referencia, mientras que las subyacentes a los casos observados son las de la población expuesta. La razón, casos observados entre casos esperados, equivale al resultado de una comparación relativa estandarizada de las tasas de incidencia de las poblaciones expuesta y de referencia utilizando como población estándar la población expuesta. La razón casos observados entre casos esperados se expresa a menudo como un porcentaje denominado «razón o índice de morbilidad (o de mortalidad) estandarizada» (IMR o SMR). Referido al ejemplo anterior tendríamos que:

IME = (50/73,35) x 100 = 68

Su utilización, en ciertos sectores, está bastante difundida. Algunos autores proponen que no se puede aplicar el principio de más vale un mal método que ninguno, sobre todo si se pretenden sacar conclusiones tras su aplicación por lo que señalan que el método indirecto «de ajuste» no ajusta por nada y debe ser evitado4.

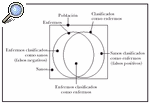
Sensibilidad y especificidad. La sensibilidad, especificidad y el valor predictivo positivo son los criterios de validez que cuantifican la capacidad de una prueba para clasificar correcta o erróneamente a una persona, según la presencia o ausencia de una exposición o de una enfermedad. Se puede considerar que, en una población, una parte de los individuos padece una determinada enfermedad, mientras que el resto de la población no la padece. De igual manera, puede asumirse que existe un método para clasificar estas dos partes de la población, pero adscribiendo algunos de los individuos sanos al grupo de los enfermos, y ciertos individuos enfermos al grupo de los sanos. La figura 1 describe este fenómeno.

Fig. 1.--Aplicación de un método diagnóstico en una población y todos sus posibles resultados.

La sensibilidad es la probabilidad de que un individuo enfermo sea clasificado como enfermo, y la especificidad, la probabilidad de que un individuo sano sea clasificado como sano.

Sensibilidad = N.º de personas enfermas que son clasificadas como enfermas/

N.º total de personas enfermas

Especificidad = N.º de personas sanas que son clasificadas como sanas/

N.º total de personas sanas

Los errores de clasificación, de acuerdo con el diagrama, pueden ser de dos tipos. Una parte de los sanos puede ser erróneamente clasificada como enfermos (falsos positivos) y una parte de los enfermos considerada como individuos sanos (falsos negativos). El valor predictivo del resultado positivo (VPP) indica la proporción de resultados correctos entre los resultados positivos de la prueba. El valor predictivo del resultado negativo (VPN) indica la proporción de resultados válidos entre los resultados negativos de la prueba. El valor global de la prueba indica la proporción de resultados válidos entre la totalidad de las pruebas efectuadas.

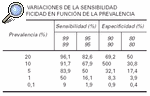
Los VPP y VPN, a igualdad de sensibilidad y especificidad, son dependientes de la prevalencia. Si la prevalencia es baja hay muchos falsos positivos, menor será el valor predictivo de los resultados positivos (VPP) y mayores los valores predictivos de resultados negativos. Si la prevalencia es alta hay un elevado número de resultados falsos negativos20.

Implicaciones en la estimación de la prevalencia. Los estudios encaminados a determinar la prevalencia de una enfermedad en una población definida se realizan a menudo examinando una muestra representativa de dicha población, y clasificando a sus componentes como enfermos o sanos. Parece razonable estimar la prevalencia a través de la proporción de la muestra que presenta la enfermedad, pero por desgracia este procedimiento puede producir resultados erróneos21-23.

Si se denomina P* a la proporción de individuos que se han clasificado como enfermos en la muestra y, como anteriormente, P a la prevalencia, puede observarse que P* tiene dos componentes: uno que procede de los individuos enfermos que se han clasificado como enfermos (verdaderos positivos), y otro que corresponde a los individuos que no tienen la enfermedad pero se han clasificado erróneamente como enfermos (falsos positivos). La proporción de individuos que es clasificada como enferma es entonces:

P* = P x sensibilidad + (1 ­ P) x (1 ­ especificidad)

Y depende, por tanto, de la prevalencia, de la sensibilidad y de la especificidad. Por ejemplo, si P = 0,01 y sensibilidad = especificidad = 0,99, P* = 0,02. Esto significa que si la prevalencia fuera estimada por la proporción que es clasificada como enferma en la muestra, el valor estimado sería de 0,02, mientras que el verdadero valor es de 0,01. El sesgo equivale a una sobreestimación del 100 %. La sobreestimación será relativamente grande para pequeñas prevalencias. La razón de este fenómeno es la siguiente: cuando la prevalencia es baja, el componente de P* que procede de la parte sana de la población tiende a ser sustancialmente importante, aunque la especificidad sea alta. La población sana puede ser 1.000 veces mayor que la población enferma, o incluso más.

Despejando P en la ecuación anterior, podríamos obtener una estimación de la prevalencia corregida en aquellas situaciones donde la sensibilidad y la especificidad son conocidas o pueden ser estimadas, siendo:

P = P* + especificidad ­ 1/ Sensibilidad + especificidad ­ 1

Ejemplo:

Un estudio de prevalencia de infecciones ungueales en pacientes afectados de psoriasis, definida como cultivo positivo, puede ilustrar este procedimiento. En la población estudiada, el 25 % de los individuos tenía cultivo positivo. El método que se había utilizado tenía una sensibilidad del 93 % y una especificidad del 91 % según datos previos. Corrigiendo el valor estimado de la prevalencia de la forma antes indicada se obtiene un nuevo valor del 19 %.

Implicaciones en el cribado. La existencia de falsos positivos y negativos debe ser considerada en la utilización de métodos de detección o cribado. La proporción de verdaderos positivos, entre aquellos que se han identificado como positivos por la prueba de cribado, se denomina valor predictivo. Siendo, como se ha explicado anteriormente, la proporción de individuos identificados como positivos P x sensibilidad + (1 ­ P) x (1 ­ especificidad) y a la fracción de este grupo que constituyen los verdaderamente positivos (P x sensibilidad), puede deducirse que:

Valor predictivo = P x sensibilidad/

P x sensibilidad + (1 ­ P) x (1 ­ especificidad)

Como se puede observar en la tabla 2, cuando la prevalencia es baja, el valor predictivo es escaso, a pesar de que los valores de sensibilidad y especificidad sean altos. Por ejemplo, el valor predictivo es sólo del 50 % cuando la prevalencia es del 5 % y la especificidad y sensibilidad son del 95 %. Esto significa que los individuos clasificados como enfermos por la prueba de cribado, sólo el 50 % serían realmente enfermos.

La utilidad de una prueba de cribado depende del coste y de los trastornos que a los individuos y a la sociedad originan las exploraciones y terapéuticas adicionales, y de los beneficios derivados del tratamiento precoz de los enfermos21-23.

TIPOS DE ESTUDIOS

Mediante el diseño de un estudio se elige el procedimiento, los métodos y las técnicas mediante los cuales el investigador selecciona a los pacientes, recoge una información, la analiza e interpreta los resultados. El diseño es, pues, la conexión entre la hipótesis y los datos8,22-26.

Los criterios para clasificar los diferentes tipos de estudio se sustentan en cuatro ejes:

1. Finalidad del estudio: analítica, todo estudio que evalúa una presunta relación causa-efecto, o descriptiva, todo estudio no enfocado en una presunta relación causa-efecto, sino que sus datos son utilizados con finalidades puramente descriptivas.

2. Secuencia: transversal, los estudios en los que los datos de cada sujeto representan un momento del tiempo, dado que las variables se han medido de forma simultánea, no puede establecerse la existencia de una secuencia temporal entre ellas, son por definición descriptivos; o longitudinal, los estudios en los que existe un lapso de tiempo entre las distintas variables, de forma que puede establecerse una secuencia temporal entre ellas; pueden ser analíticos o descriptivos; en los estudios analíticos debe tenerse en cuenta si la secuencia temporal es de causa hacia desenlace (estudios experimentales y estudios de cohortes), o bien de desenlace hacia causa (estudios de casos y controles).

3. Control de la asignación de los factores de estudio: experimental en los que el observador asigna el factor de estudio y lo controla de forma deliberada para la realización de la investigación, se centran en una relación causa-efecto (analíticos) y en general evalúan el efecto de una o más intervenciones preventivas o terapéuticas, u observacional, el factor de estudio no es asignado por los investigadores, sino que éstos se limitan a observar, medir y analizar determinadas variables, sin ejercer un control directo sobre el factor de estudio.

4. Inicio del estudio en relación a la cronología de los hechos: prospectivo, aquellos estudios cuyo inicio es anterior a los hechos estudiados, de forma que los datos se recogen a medida que van sucediendo, o retrospectivo, estudios cuyo diseño es posterior a los hechos estudiados27.

Estudios observacionales

Se trata de aquellos estudios en el que en el investigador no controla la asignación, la asignación no se realiza de manera aleatoria y no existe intervención en el diseño (fig. 2). Los estudios observacionales se dividen en descriptivos y analíticos.

Fig. 2.--Tipos de diseños. (Modificada de Burgos Rodríguez28 y Guallar39.)

Estudios descriptivos

La principal finalidad de estos estudios es describir la frecuencia y las características de un problema de salud en una población, describir la asociación entre dos o más variables, sin asumir una relación causal entre ellas, y generar hipótesis razonables que deberán ser contrastadas mediante estudios analíticos28. Desde el punto de vista de la evidencia científica, en la que las escalas de clasificación diferencian de forma jerárquica los distintos grados de evidencia, en función de los diversos tipos de diseños para determinar la existencia de una relación causal, son los estudios que demuestran una menor evidencia (tabla 3)6-8,10,24,27,29.

Informes de casos y series de casos. Esta aproximación descriptiva se basa en la experiencia clínica de un paciente o grupo de pacientes con un diagnóstico similar. Es posible que se identifique una característica inusual de la enfermedad o de los antecedentes del o de los enfermos. Este tipo de estudios sirven para lanzar una primera hipótesis, que después se verifica o no, con otro tipo de estudios, o pueden ser la primera señal de alarma respecto a la aparición de nuevos síndromes o epidemias.

Por ejemplo: en 1981, en la ciudad de Los Ángeles, se observó un número extrañamente alto de ingresos por sarcoma de Kaposi y, en otros casos, de neumonía por Pneumocystis carinii, en personas jóvenes previamente sanas; como denominador común, en ese exceso de pacientes había hombres homosexuales, de ámbito urbano, y sin experiencia previa de inmunosupresión; todos conocemos que fue el inicio del SIDA30.

Aún cuando podrían citarse muchos otros ejemplos de interés, se calcula que en España las publicaciones de este tipo suponen entre el 60 y el 80 % de la producción científica médica, y su utilidad tiene una serie de limitaciones31. En principio, no sirven para probar hipótesis estadísticas, dado que representan la experiencia de una sola persona o un pequeño número de ellas24. Desde el punto de vista epidemiológico presentan un problema crucial: la inexistencia de algún grupo que puede servir como comparación o control28,32.

Estudios ecológicos. Los diseños ecológicos usan medidas que relacionan características de población en su conjunto, y permiten describir los problemas de salud basados en criterios geográficos o temporales. Una clasificación de los estudios ecológicos los presenta en tres grandes grupos:

1. Descriptivos o exploratorios. Comparan incidencia o prevalencia de un determinado problema en varias áreas, buscando la detección de patrones de tipo geográfico. Un buen ejemplo lo constituyen los denominados «Atlas de Cáncer»33. La observación de algunas diferencias según un patrón geográfico puede dar lugar a la generación de hipótesis sobre factores sociales, culturales, económicos, de hábitos de vida.

2. Estudios de series temporales. Describen el comportamiento de los problemas a lo largo del tiempo, buscando patrones estacionales, así como tendencias o cambios de tendencias a más largo plazo. Por ejemplo, el análisis de la incidencia del carcinoma escamoso muestra un incremento de la incidencia entre el año 1984 y 1992. El aumento fue global durante todo ese período, una tendencia ascendente significativa34.

3. Estudios de correlación ecológica. Se obtiene, de cada una de las unidades de análisis, una medida sintética de la frecuencia de la enfermedad (p. ej., la incidencia, la prevalencia o la mortalidad) y una medida sintética de la frecuencia de la exposición a uno o varios factores. El análisis se centra en determinar si las unidades ecológicas con alta frecuencia de la enfermedad también tienen tendencia a un mayor grado de exposición. Estos estudios son útiles cuando no se dispone de información individual. Esta correlación puede realizarse sobre datos referidos a un mismo momento del tiempo (p. ej., relacionar la mortalidad por infarto agudo de miocardio y el consumo de cigarrillos per cápita en los países europeos en un año determinado).

La característica fundamental de los estudios ecológicos es que no se dispone de información individual sobre exposición y la enfermedad individual. Las ventajas son la rapidez, facilidad y economía de esfuerzos. A pesar de sus limitaciones, este tipo de estudios son útiles para generar hipótesis.

La principal limitación es la llamada «falacia ecológica», que se debe a la existencia de errores, derivados fundamentalmente del intento de extrapolar hallazgos de tipo ecológico a situaciones individuales, o cuando resultados provenientes de ciertos subgrupos se infieren a la totalidad de la población que los origina. Burgos cita como ejemplo el estudio que demuestra que la disminución en el número de nidos de cigüeña es capaz de predecir un descenso en la natalidad, cuando en el citado estudio no se tiene en cuenta el grado de urbanización o de industrialización28,35-37.

Estudios transversales (prevalencia). Se trata de estudios que tienen como finalidad la estimación de la prevalencia de una enfermedad o una característica en una población. Se basan en la definición precisa de una población de estudio y en la obtención de una muestra representativa de ella. Este tipo de estudios supone un paso más en relación a los diseños previamente comentados, no describen simplemente qué ocurre en una serie de casos, y además se dispone de información sobre todos los individuos investigados o una muestra de ellos.

Las ventajas de los estudios transversales es que dan una descripción de la magnitud y el alcance del problema; es la «fotografía» de la situación en un momento determinado, son útiles en la evaluación de intervenciones sobre la población, pueden identificar casos (las personas con el efecto) y no casos (el resto), lo que da pie a un posible análisis como si se tratara de estudios de casos y controles, y una de las mayores ventajas no suficientemente valorada en la literatura es el bajo coste de este tipo de diseños28,35-37.

Estudios analíticos

Los estudios descriptivos dan lugar a hipótesis variadas. El siguiente paso consiste en verificarlas, en este momento el investigador tiene la posibilidad de acudir a los diseños analíticos, estos estudios reúnen un conjunto de alternativas suficientemente potentes frente a los estudios experimentales. A la hora de comparar la incidencia de enfermedad entre los individuos expuestos y no expuestos a un determinado factor se dispone por lo general de dos estrategias distintas. Estas dos formas de abordar el problema son los llamados estudios de seguimiento o cohortes y los estudios de casos y controles. El estudio de cohortes representa el método más sencillo y directo38-45.

Estudios de cohortes. La idea central en este tipo de diseños es la observación a lo largo del tiempo de un grupo de personas en las que el efecto que se investiga no está inicialmente presente y los sujetos de la población de estudio son examinados y clasificados como expuestos o no expuestos. Tras el período de seguimiento se compara la frecuencia con que aparece el efecto o respuesta en los expuestos y no expuestos. En ocasiones se consideran varias categorías de exposición, por ejemplo: no expuestos, poco expuestos y muy expuestos. A cada uno de los grupos de estudio se le denomina cohorte. La aportación que introduce este tipo de estudios es el carácter longitudinal del diseño en el tiempo.

El grupo no expuesto aporta información sobre la incidencia que podría esperarse en el grupo expuesto si dicha exposición no influyese en la aparición de la enfermedad. Teniendo esto en cuenta, el grupo no expuesto debe seleccionarse de manera que sea similar al grupo expuesto respecto a otros factores de riesgo para la enfermedad en estudio. En principio existen tres formas de selección del grupo no expuesto:

1. Comparación interna. Se elige una cohorte que contiene individuos expuestos y no expuestos en número suficiente.

2. Comparación externa. Una vez identificada la cohorte expuesta se busca una cohorte no expuesta que sea similar.

3. Comparación con la población general. La cohorte expuesta es comparada con el total de la población; por ejemplo con el total del país (considerado como no expuesto).

El interés aquí es conocer en qué medida la incidencia en los expuestos es mayor, menor o igual que en los no expuestos. Estas medidas, riesgo relativo (expresado como razón de riesgos y razón de tasas), o razón de oportunidades y las medidas de impacto potencial como riesgo atribuible y sus fórmulas para calcularlas quedan lejos del objetivo de esta monografía y remitimos al lector interesado a los tratados sobre el tema40-45.

Estudios de casos y controles. La frecuencia de aparición de nuevos casos en la mayoría de las enfermedades es baja. Para obtener un número suficiente de casos en un estudio de cohortes es necesario examinar y seguir a un gran número de individuos de cada estado de exposición durante un largo período. El coste económico es entonces muy elevado. Una alternativa más económica consiste en estudiar los datos de exposición utilizando una muestra de la población en estudio en lugar del total de ésta, los estudios de casos y controles.

En los estudios de casos y controles se elige un grupo de individuos que tienen un efecto o una enfermedad determinada (casos) y otro en el que está ausente (controles). El criterio de asignación es ahora la presencia o no del efecto. En realidad, un estudio caso control tiene enormes semejanzas con uno de cohortes, pero aquí se obtiene información sobre la distribución de la exposición a partir de una muestra de la población en estudio o de la base del estudio.

La selección de los casos tiene como objetivo incluir todos los casos incidentes detectados en una población bien definida durante un período de tiempo. En la selección de los casos el requisito más importante es que sean casos nuevos, es decir, casos incidentes, para lo cual se necesita además un criterio diagnóstico específico que delimite los criterios de inclusión junto a la definición de caso. La selección de los controles es el punto más difícil en el diseño. El grupo control debe ser seleccionado de forma que refleje la distribución de la exposición en la población a estudio, es decir, en la población que genera los casos. A la hora de la selección existen dos posibilidades:

1. Realizar un muestreo aleatorio de la población a estudio. Esto requiere que dicha población (población origen de los casos) sea susceptible del muestreo. En este caso los controles serán representativos de la población de estudio en sentido estricto (estadístico), y la selección en sí misma no introduce ningún error sistemático.

2. Los controles no son seleccionados como una muestra aleatoria de la población en estudio. Es la única alternativa cuando los casos son elegidos de forma que la población en estudio no es accesible a muestreo aleatorio. Por ejemplo, cuando los enfermos diagnosticados en un hospital constituyen el grupo de casos, probablemente estos pacientes no representan a todos los afectados por esta enfermedad en la población origen de la muestra. El problema estriba en que los controles así seleccionados podrían no reflejar la distribución de la exposición en la población a estudio, y esto introduciría un error sistemático46-49.

Estudios experimentales

Los estudios experimentales abarcan un conjunto de diseños en los que existe una intervención planificada por los investigadores y hay algún control sobre la asignación de los pacientes, aunque como veremos, no siempre están presentes ambos aspectos. Para algunos autores representan el mejor tipo de estudio cuando se pretende verificar una hipótesis, por sus características; el experimento permite el control de la asignación, la inclusión de manera aleatoria de las personas en los grupos tiene una ventaja sobre el resto de las estrategias: si el azar no desempeña una mala pasada, se puede esperar que los grupos de comparación sean muy similares entre sí. Es decir, para múltiples variables (como sexo, edad y demás) es posible conseguir grupos homogéneos, en los que la distribución de las variables que podrían interferir en los resultados sea semejante. De esta forma, si se encuentran diferencias, sólo quedaría una explicación: la intervención, o manipulación de una variable. La situación ideal la representa pues el estudio aleatorio controlado28,32,35,50-53.

Aun cuando los estudios experimentales pueden parecer enormemente atractivos por sus ventajas, en multitud de ocasiones son impracticables, las razones éticas impiden exponer a seres humanos a situaciones que pudieran ser perjudiciales para ellos. A pesar de parecer superiores, los estudios experimentales también presentan errores. Es clásico recordar cómo el cirujano Hunter, escéptico ante la doctrina unicista que defendía que la sífilis era una manifestación tardía de la gonococia, decidió hacer un experimento autoinoculándose pus de un enfermo con gonococia; a los pocos días desarrolló una uretritis y a las 4 semanas un chancro sifilítico. Determinó de manera errónea que la doctrina unicista era verdadera y que el método experimental la apoyaba. Hoy en día conocemos que Hunter se inoculó con material de un paciente con las dos enfermedades y que la coexistencia de varias enfermedades de transmisión sexual en un mismo enfermo es un fenómeno frecuente26.

Estudios cuasi experimentales. Se definen como estudios experimentales en los que falta o bien la asignación aleatoria o bien el grupo control. Se trata de responder a la pregunta, ¿consigue la intervención producir alguna diferencia? Las intervenciones a evaluar pueden ser muy diversas. Por ejemplo, interesa saber si el tipo de información que se facilita a los pacientes con psoriasis influye sobre su calidad de vida. En situaciones de este tipo puede medirse algún indicador de la situación (lo que en cuasi experimentación se conoce como indicador de estado del sistema). A continuación se introduce alguna modificación (la intervención), y una segunda observación mide de nuevo la situación. La diferencia entre la primera y la segunda observación determina si la modificación tiene algún efecto28,53,54.

Ensayos clínicos o estudios aleatorios controlados. Son el experimento en las condiciones de control más ideales. Se realizan mediante asignación aleatoria individual, de forma que el investigador decide la exposición o no de los participantes usando el azar como criterio (una moneda al aire, tablas de números aleatorios o técnicas de ordenador). Se espera que el azar distribuya a las personas de forma homogénea, consiguiendo grupos comparables, similares en todo excepto en la exposición de interés. La manipulación de una variable consigue entonces que en uno de los grupos esté presente la exposición y en otro, que se usa como referencia o control, no lo esté. De esta forma, las diferencias que se encuentren al final del estudio pueden atribuirse al efecto de la exposición. De acuerdo con los objetivos perseguidos, la investigación de estudios clínicos con fármacos se desarrolla en fases (tabla 4)38,45.

CALIDAD DE LOS ESTUDIOS EPIDEMIOLOGICOS

Un estudio epidemiológico puede ser considerado como un ejercicio de medida de la frecuencia de una enfermedad, o del efecto que sobre ella tiene una determinada exposición. Existen tres conceptos que hoy en día se consideran fundamentales para realizar e interpretar investigación clínica: la validez interna, la precisión estadística y la validez externa. La validez se refiere a la capacidad del estudio para medir el objetivo que se propone, o bien el grado en que una variable mide realmente aquello para lo que está destinada. Su defecto determina desviaciones denominadas «error sistemático». Cuanto menos válida sea una medida más probabilidades hay de cometer un sesgo o error sistemático. La precisión es la posibilidad de replicación o reproducción de un estudio, es decir, el grado de similitud que presentarían los resultados en distintos estudios realizados bajo las mismas circunstancias, es decir, cuanto mayor es la precisión, menor es el papel que el azar desempeña en el resultado obtenido en un estudio. La falta de precisión se denomina «error aleatorio», es decir, errores producidos por el azar debidos al hecho de no trabajar con poblaciones completas, sino con muestras de éstas; este tipo de error disminuye al aumentar la muestra.

Todo estudio clínico es pues susceptible de cometer los dos tipos de errores antes mencionados, los errores sistemáticos o sesgos conllevan siempre que la validez interna del estudio sea baja y también pueden -resultar en una validez externa baja. Los errores aleatorios resultan en la falta de precisión estadística y en una significación estadística baja. Así pues, las preguntas que nos hacemos al valorar el resultado de un estudio son tres. La primera y la más importante es si el resultado de aquel estudio es correcto (validez interna). En caso afirmativo, procede hacerse la segunda pregunta, cuán precisa o estadísticamente significativa es la respuesta que da al problema planteado (hasta qué punto los resultados obtenidos pueden deberse al azar). La tercera pregunta es si el resultado es aplicable a nuestros propios pacientes (validez externa)9,36,55.

VALIDEZ DE LAS COMPARACIONES DE FRECUENCIAS DE ENFERMEDAD

En los últimos años se han clasificado los errores sistemáticos en los diseños de los estudios en tres grandes grupos: los sesgos de selección, los sesgos de información y los factores de confusión. Como ya se señaló, estos factores conducen a una estimación incorrecta o no válida del efecto o parámetro que se estudia9,19,22,26,33,56.

Sesgo de selección

Este tipo de error ocurre en fases del estudio al elegir una muestra que no represente de forma adecuada a la población de estudio o al formar los grupos que se van a comparar. Por ejemplo:

Deseamos estimar la prevalencia del cáncer cutáneo en los sujetos adultos residentes en un municipio (población de estudio). Para ello, se estudian los 100 primeros sujetos que acuden a una consulta de un servicio dermatológico. Obviamente, los sujetos que acuden a la consulta no son representativos de la población del municipio, por lo que obtendríamos una estimación sesgada de la prevalencia de la enfermedad.

Los sesgos de selección también se pueden producir durante el seguimiento de los participantes. Si la proporción de individuos que se pierden es diferente en los grupos que se comparan, el investigador sospechará que puede existir un sesgo. No obstante, esta diferencia no implica que exista, sino que el error se producirá si la probabilidad de desarrollar la enfermedad entre los sujetos que se pierden es diferente en cada uno de los grupos. Por ejemplo:

Un estudio que compara dos antifúngicos, administrado cada uno a un grupo de 100 sujetos, y se producen 20 pérdidas en cada uno de ellos. El porcentaje de éxito terapéutico con cada uno de ellos es del 50 % entre los que finalizan el estudio, por lo que se podría concluir que poseen la misma eficacia (50 %). Sin embargo, entre las pérdidas (20 pacientes) sólo uno de los sujetos que recibió el medicamento 1 fue clasificada como éxito mientras que con el medicamento 2, lo fueron 10 pacientes. Cuando se calcula el tanto por ciento total de éxitos el medicamento 2 es el más eficaz (50 de 100 = 50 % frente a 41 de 100 = 41 %). Así pues, aunque el porcentaje de pérdidas sea el mismo, se puede producir un sesgo.

Otra situación que puede producir un sesgo de selección es la existencia de no respuestas, lo que suele ocurrir en las encuestas. Por ejemplo:

Supongamos un estudio en el que se desea determinar el tratamiento de primera elección de dermatitis atópica grave entre los dermatólogos de una determinada zona geográfica. Para ello se selecciona una muestra aleatoria de 100 profesionales a los que se envía un cuestionario. Comprueban 60 dermatólogos, de los que 30 comprueban que el tratamiento de primera elección son los corticoides de potencia intermedia. De este resultado no puede inferirse automáticamente que la utilización de corticoides tópicos como primera elección es del 50 %. Hay que tener en cuenta la existencia de 40 dermatólogos que no han comprobado a la encuesta. Si la utilización de corticoides entre los que no han respondido es diferente de la que existe entre los que sí han respondido la cifra del 50 % es una estimación sesgada de la verdadera prevalencia. En caso contrario, podría asumirse que las no respuestas no están relacionadas con el fenómeno de estudio (podrían considerarse aleatorias), de forma que la cifra observada sería una estimación no sesgada, aunque se habría producido una pérdida de precisión en la estimación debido al menor número de respuestas.

La única manera de asegurar que las pérdidas durante el seguimiento o las no respuestas no introducen un error sistemático en los resultados es evitar que se produzcan, o bien obtener información suplementaria que permita evaluar si los sujetos que se pierden, o que no comprueban, difieren de los que finalizan el estudio5.

Sesgos de información

El sesgo de información se produce cuando las mediciones de las variables de estudio son de mala calidad o son sistemáticamente desiguales entre los grupos de pacientes. Las principales fuentes de estos errores son la aplicación de pruebas poco sensibles y/o específicas para la medición de las variables o de criterios diagnósticos incorrectos, o distintos en cada grupo, y las imprecisiones u omisiones en la recogida de datos. Por ejemplo:

Supongamos un estudio en el que el objetivo es comparar el PASI en pacientes con psoriasis en función del sexo. Sin embargo, la medición en las mujeres se hace completamente desnudas, mientras que la persona responsable de medirlo en los hombres realiza la medición a los pacientes con zapatos, calcetines y calzoncillos. El problema de este estudio es que se aplica un mismo instrumento de medida de forma diferente según el grupo de estudio. Otro ejemplo: si se quiere estudiar una asociación entre la ingestión de alcohol y la psoriasis, y en los pacientes con psoriasis se obtiene la información a partir de una entrevista personal, mientras que en los individuos del grupo control se obtiene de las historias clínicas, es de esperar que en el primer grupo la información sea más exacta y sistemáticamente diferente de la obtenida en el grupo control, lo que sesgará los resultados.

Por otra parte, se ha definido como sesgo de sospecha diagnóstica el hecho de que el conocimiento de que el paciente ha estado expuesto a un factor de riesgo condicione la intensidad con la que se investiga un determinado diagnóstico8. Por ejemplo:

Si conocemos que un paciente con virus de la inmunodeficiencia humana (VIH) ha estado tomando sulfamidas y presenta una erupción cutaneomucosa generalizada de 5 semanas de evolución es más probable que pensemos en un síndrome de Stevens-Johnson que si desconocemos tal exposición.

Los errores sistemáticos, ya sean de selección o de información, a diferencia de lo que ocurre con el error aleatorio, no se atenúan al aumentar el tamaño de la muestra; de hecho, aunque se incluyan más individuos lo único que se logrará es perpetuar el sesgo. Además, un error de estas características, una vez introducido, es casi imposible de enmendar en la fase de análisis5.

Sesgos de confusión

Se trata del tercer tipo de sesgo que pone en peligro la validez interna de un estudio clínico. No se tiene en cuenta que la asociación observada entre un factor de estudio (un fármaco, un hábito de vida o cualquier otro factor de riesgo) y la variable de la respuesta (una enfermedad, un tratamiento, un diagnóstico) puede ser total o parcialmente explicada por una tercera variable (factor de confusión), o por el contrario, cuando una asociación real queda enmascarada por este factor. Por ejemplo:

En un estudio epidemiológico se descubrió que los individuos con alto consumo de alcohol tenían mayor riesgo de padecer cáncer de pulmón que los abstemios. Sin embargo, la causa de este aumento de riesgo es debida al mayor consumo de tabaco entre los bebedores; la confusión introducida por el tabaco explicaba la asociación observada entre consumo de alcohol y cáncer de pulmón57.

En la situación más extrema, un factor de confusión puede invertir la dirección de una asociación. Es la llamada paradoja de Simpson. Rothman56 presenta el siguiente ejemplo: supongamos que un hombre entra en una tienda para comprarse un sombrero y encuentra una estantería con 30, 10 de ellos negros y 20 grises. Descubre que 9 de los 10 sombreros negros le están bien, pero que de los 20 grises sólo le están bien 17. Por tanto, toma nota de que la proporción de sombreros negros que le están bien es del 90 %, mientras que la de los grises es sólo del 85 %. En otra estantería de la misma tienda encuentra otros 30 sombreros, 20 negros y 10 grises. En ella, 3 (15 %) de los sombreros negros le va bien y de los grises sólo 1 (10 %) le va bien. Antes de que escoja un sombrero la tienda cierra y él decide volver al día siguiente. Durante la noche un empleado ha puesto todos los sombreros en una única estantería: ahora hay en ella 60 sombreros, 30 de cada color. El cliente recuerda que el día anterior la proporción de sombreros negros que le estaban bien era superior en ambas estanterías. Hoy se da cuenta de que aunque tiene delante los mismos sombreros, una vez mezclados sólo un 40 % (12 de 30) de los sombreros negros le está bien, mientras que de los grises es del 60 % (18 de 30). Algunos autores consideran este tipo de sesgo distinto de los anteriores, ya que es el único que se puede controlar en la fase de análisis y no sólo en la de diseño5,9,26,46,47,58.

Control de los errores

Los sesgos de selección y de clasificación deben controlarse en la medida de lo posible durante la fase de diseño del estudio o, de lo contrario, pueden llegar a invalidar los resultados. La confusión también puede controlarse en la fase de diseño. Se utiliza en ocasiones la restricción, es decir, la limitación del estudio a un solo subgrupo. Si el sexo fuera un factor de confusión ya conocido, se puede centrar el estudio en hombres o mujeres únicamente. Otra posibilidad de control es mediante lo que se conoce como apareamiento, haciendo que los grupos de comparación sean similares en cuanto a factores de confusión ya conocidos; por ejemplo, elegir cada control con una edad semejante al caso correspondiente. La mejor herramienta en el diseño es, sin embargo, la asignación en los grupos de manera aleatoria26,43.

PRINCIPIOS BASICOS DEL ANALISIS DE DATOS

Los estudios epidemiológicos se dividen en dos grupos según sus objetivos. El primero reúne aquéllos dirigidos a determinar la frecuencia de enfermedad en una población.

Medidas de frecuencia de enfermedad

Los estudios que describen la frecuencia de enfermedad utilizan la prevalencia, la incidencia acumulada o la tasa de incidencia como medidas de ésta. Los valores obtenidos deben presentarse acompañados de un «intervalo de confianza» que informa sobre la precisión del valor observado59,60. Un intervalo de confianza del 95 % es un rango de valores calculado teniendo en cuenta la variación aleatoria; este intervalo tiene un 95 % de probabilidades de contener el verdadero valor del parámetro estudiado. Esto significa que, en promedio, el 95 % de los intervalos contienen el valor real y el 5 %, no. El intervalo de confianza informa acerca de la precisión del estudio. Esto es de gran importancia en los estudios epidemiológicos en los que la variación aleatoria derivada del reducido número de enfermos estudiados desempeña un papel importante a la hora de interpretar los resultados. De esto se deduce que el aumento del número de individuos produce un estrechamiento del intervalo y aumenta así la precisión de la estimación5.

En el cálculo del intervalo de confianza se asume que se ha estudiado una muestra aleatoria de la población de referencia. Al interpretarlo, hay que tener en cuenta la posibilidad de existencia de otras fuentes de error no debidas al azar. Si éstas existen, o si la muestra no es aleatoria, el error de la estimación puede ser mayor que el sugerido por la amplitud del intervalo5. Para una discusión detallada sobre el cálculo y la interpretación de un intervalo de confianza, el lector puede dirigirse a un texto de estadística61,62.

En el cálculo del intervalo de confianza es necesario utilizar un modelo probabilístico mediante el cual se estima la probabilidad de obtener distintos resultados posibles. En epidemiología, el modelo utilizado se basa generalmente en la distribución binomial o en la distribución de Poisson. Sin embargo, en la práctica, cuando el tamaño es grande, estos modelos pueden aproximarse a la distribución gaussiana, llamada generalmente distribución normal. Por tanto, asumiendo que el tamaño muestral es suficientemente grande, los intervalos de confianza pueden obtenerse utilizando los siguientes procedimientos:

A.Prevalencia. Llamamos B al número de individuos que presentan la enfermedad y N al número total de individuos en la población; según la definición antes enunciada, la prevalencia sería:

P = B/N

El intervalo de confianza del 95 % se obtendría como:

P ± 1,96 √P(1 ­ P)/N

Donde operando con los signos + y ­ se obtienen respectivamente los límites superior e inferior del intervalo. La constante 1,96 corresponde al nivel de confianza deseado del 95 %.

B.Incidencia acumulada. Denominando A al número de individuos que enferman durante el período de observación y N al número de individuos en riesgo al comienzo de dicho período, tendríamos que:

IA = A/N

El intervalo de confianza del 95 % se obtiene de acuerdo con los mismos principios, ya que tanto la prevalencia como la incidencia acumulada son proporciones:

IA ± 1,96 √IA(1 ­ IA)/N

C.Tasa de incidencia. Si denominamos A al número de casos que aparecen durante el período de observación y R al número de años en riesgo, la tasa de incidencia sería:

I = A/R

El intervalo de confianza correspondiente vendría dado por:

I ± 1,96 √I/R

Desde el punto de vista estadístico existe una diferencia importante entre las dos medidas anteriores y la tasa de incidencia, dado que las primeras son proporciones mientras que la tasa de incidencia es el número de casos por unidad de tiempo en riesgo6,10,28.

EVALUACION Y APLICACION DE LOS RESULTADOS DE ESTUDIOS DE PRUEBAS DIAGNOSTICAS

Los clínicos habitualmente tenemos dilemas cuando ordenamos e interpretamos pruebas diagnósticas. La continua proliferación de tecnología médica proporciona cada vez más artículos sobre pruebas diagnósticas. Este apartado presenta los principios de artículos bien realizados sobre pruebas diagnósticas y la óptima utilización de la información que proporcionan (tabla 5)63-67.

¿Son válidos los resultados del estudio?

Guía primaria

¿Existe una comparación ciega, independiente con una prueba de referencia estándar? La utilidad de una prueba diagnóstica se determina mejor cuando se compara con la «verdad». El lector debe asegurarse que la prueba de referencia estándar (biopsia, autopsia, seguimiento prolongado, etc.) se ha aplicado a todos los pacientes junto con la prueba bajo estudio7. Si la prueba estándar de control no es aceptable el artículo no proporcionará resultados válidos. Si se acepta la referencia estándar, la siguiente pregunta es si los resultados de la prueba y la prueba de referencia son aplicados de forma independiente.

¿El paciente individual se incluye en un apropiado espectro de pacientes a los que la prueba diagnóstica se puede aplicar en la práctica clínica? Una prueba diagnóstica es realmente útil sólo si distingue entre enfermos y sanos o estados de la enfermedad que pueden confundirse. Casi todas las pruebas pueden distinguir entre sano y enfermedad muy avanzada o grave, pero esto no es de utilidad en la práctica clínica diaria. El verdadero, valor pragmático de una prueba se establece sólo en un estudio que se asemeje de manera cercana a la práctica clínica. Un ejemplo clásico de prueba diagnóstica es el antígeno carcinoembrionario (CEA) en el cáncer colorrectal. Inicialmente se midieron las concentraciones de CEA en pacientes que presentaban un carcinoma colorrectal en estado avanzado, obteniéndose cifras elevadas en el 97,2 % de los pacientes. Estos resultados sugirieron que podía ser una prueba de utilidad para el diagnóstico o incluso un cribado del cáncer colorrectal. Estudios posteriores en enfermos con estadios menos avanzados de cáncer colorrectal y otras enfermedades inflamatorias demostraron que la eficacia del CEA era nula, quedando en estos momentos el CEA únicamente como elemento de seguimiento de pacientes con cáncer colorrectal conocido68. Algo similar ocurre en nuestra especialidad con el marcador serológico S-100 en sangre para el melanoma que es incapaz de detectar estadios precoces de la enfermedad y no es de utilidad como prueba de cribado69.

Guía secundaria

¿Se ha evaluado la influencia para realizar la prueba estándar de los resultados obtenidos por la prueba? Las propiedades de una prueba diagnóstica estarán distorsionadas si sus resultados influyen para que los pacientes realicen la prueba de referencia estándar.

¿Los métodos para realizar la prueba están lo suficientemente detallados como para permitir su replicación? Si los autores de un artículo concluyen que podemos usar un prueba diagnóstica, deben explicar cómo podemos realizarla. Esta descripción debe abarcar todos los aspectos que son importantes en la preparación del paciente, la realización de la prueba (técnica, posibilidad de dolor), y el análisis e interpretación de resultados.

¿Cuáles son los resultados? ¿Se proporcionan los datos necesarios para realizar los cálculos de los resultados proporcionados por la prueba? Todo artículo debe proporcionar los datos necesarios (sensibilidad, especificidad, likelihood ratios) suficientes que nos permitan realizar los cálculos necesarios para obtener los mismos resultados.

¿Los resultados presentados me ayudarán en la atención a mis pacientes? ¿Se podrán reproducir los resultados y su interpretación en mi consulta? El valor de las pruebas depende de su habilidad para lograr los mismos resultados cuando se aplican al mismo tipo de pacientes. Una pobre reproducibilidad puede deberse a la prueba en sí misma o a que la aplicación de la prueba requiere interpretación. Idealmente, un artículo debe informar cuán reproducible es una prueba; esto es especialmente importante cuando se requiere una experiencia para la realización o interpretación de la prueba (podemos trasladar este problema cuando uno o más colegas examinamos el mismo paciente, la misma preparación histológica, incluso cuando todos son expertos en el tema y no se llega al mismo diagnóstico). Si la reproducibilidad de una prueba es mediocre y muestra discordancias entre observadores y aun así la prueba discrimina bien entre aquellos con la enfermedad y los que no, es entonces muy útil. Bajo estas circunstancias, es probable que la prueba sea fácilmente aplicable en nuestra consulta.

¿Se pueden aplicar los resultados a mis pacientes? Si se practica la medicina en pacientes similares a los del estudio y los pacientes reúnen todos los criterios de inclusión y ninguno de los de exclusión, se puede confiar en que los resultados son aplicables. Hay que tener en cuenta que las propiedades de la prueba pueden cambiar con diferentes intensidad de las enfermedades o condiciones parecidas.

¿Cambian los resultados de la prueba mi manejo? Es útil hacer, aprender, enseñar y comunicar decisiones de manejo del paciente para unir las posibilidades de una prueba a la enfermedad diana en estudio; es por ello que, para una enfermedad diana, una prueba muestra un resultado debajo de un umbral que permite al clínico descartar un diagnóstico y no solicitar nuevas pruebas (umbral de diagnóstico). De forma similar, hay resultados por encima de un umbral que permiten al facultativo considerar un diagnóstico confirmado y no solicitar nuevas pruebas e iniciar tratamiento (umbral de tratamiento). Cuando la probabilidad de que la enfermedad diana se encuentre en la prueba entre el umbral de diagnóstico y el umbral del tratamiento, es obligatorio realizar nuevas pruebas que confirmen el diagnóstico.

Es necesario señalar que, en medicina clínica, estamos realizando desde el inicio una serie secuencial de varias pruebas. Cada pregunta de la historia, o cada hallazgo de la exploración física, representa una prueba diagnóstica. Vamos generando diagnósticos que se van modificando con cada nuevo hallazgo. En general, también pueden usarse pruebas de laboratorio o procedimientos radiológicos de la misma forma. Sin embargo, si dos pruebas están muy cercanas entre sí, la aplicación de la segunda prueba puede proporcionar poca o nula información añadida. Por ejemplo, si se dispone de los resultados de la prueba más potente para la detección del déficit de hierro, la ferritina sérica, prueba adicionales como el hierro sérico o la saturación de transferrina no añaden nueva información70.

¿Estarán los pacientes mejor con los resultados de la prueba? El criterio último para la utilidad de una prueba diagnóstica es si añade información no disponible de otra manera, y si esta información lleva a un cambio en el tratamiento del paciente que beneficie al paciente. El valor de una prueba será indiscutible cuando la enfermedad sin diagnóstico apropiado es grave, la prueba no supone importantes riesgos y existe un tratamiento efectivo71.