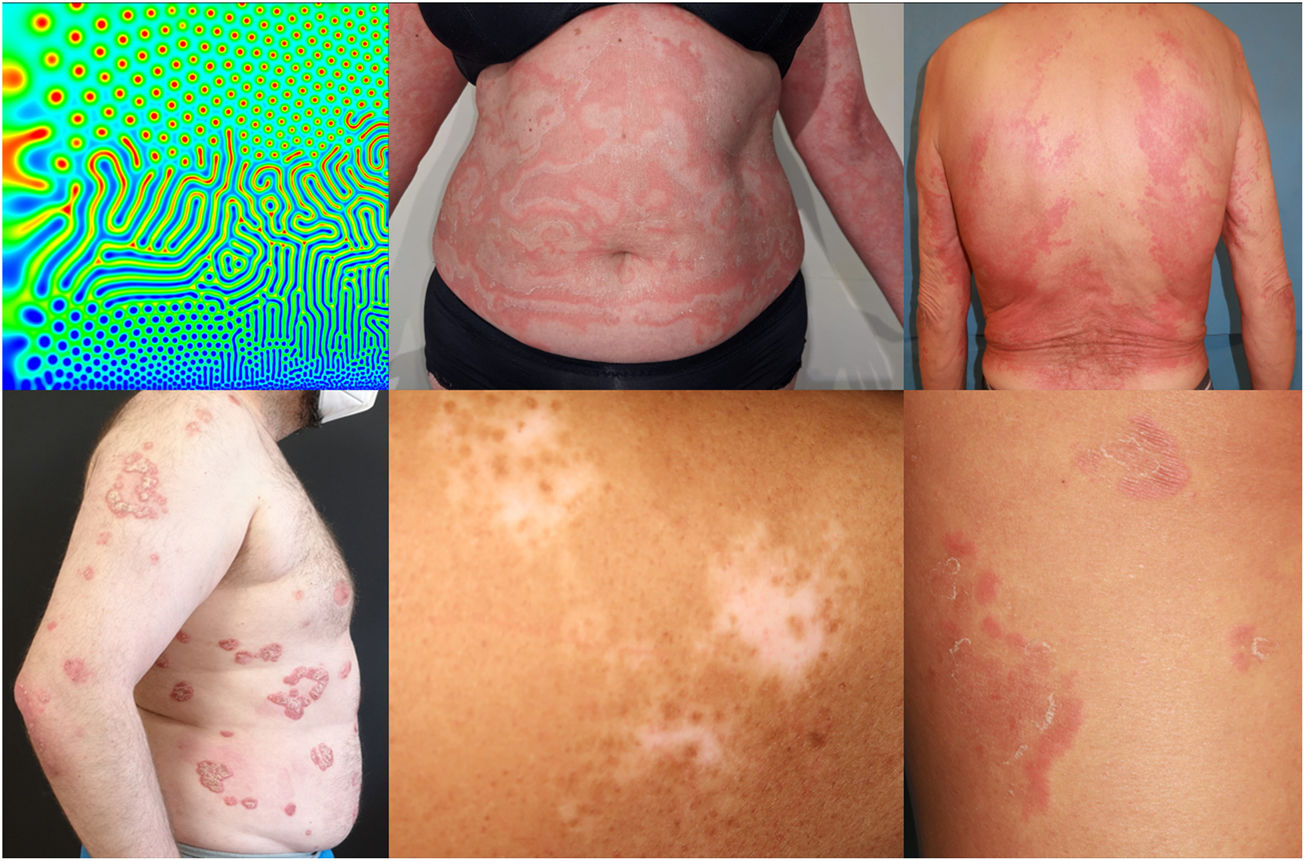
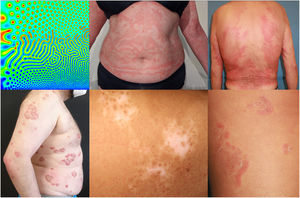
Los sistemas de reacción-difusión fueron propuestos por Alan Turing en su artículo de 1952 titulado: «Fundamentos químicos de la morfogénesis». Este modelo matemático explica cómo se desarrollan múltiples patrones espaciales complejos. Se basa en la existencia de dos o más sustancias, llamadas morfógenos, que difunden a través de un medio continuo e interaccionan entre sí. Según el tipo de interacción, se forman los diferentes patrones de manera estocástica. Se pueden representar de manera simplificada mediante la siguiente fórmula:
donde cada componente del vector q(x,t) representa la concentración de una sustancia, D es una matriz diagonal de coeficientes de difusión, Δ denota al operador laplaciano, y R representa las reacciones locales (fig. 1).
En función de las dinámicas de las reacciones resultantes y de su longitud de onda, existen seis estados potenciales distintos. En el caso VI, también conocido como patrón de Turing (PT), se forma una onda no lineal en equilibrio dinámico, cuya longitud está determinada por las interacciones entre las sustancias y sus tasas de difusión. Estos PT surgen de manera autónoma y tienden a regenerarse por sí solos ante alteraciones1.
Los PT combinan un sistema de retroalimentación positiva y un sistema de retroalimentación negativa. Al variar la cantidad y tipos de sustancias, se logran formar patrones casi infinitos. Las sustancias pueden ser entidades simples como moléculas, o complejas como circuitos de señalización celular. Además, se ajustan a la difusión en diferentes medios como fenómenos de quimiotaxis y potenciales de acción celulares.
La distribución del plumaje en las aves, el desarrollo embrionario de las extremidades y del árbol bronquial, son ejemplos de PT en la naturaleza2. Las características de los PT son más evidentes en modelos en dos dimensiones, como la piel. Algunos ejemplos son el patrón moteado del guepardo y las rayas de las cebras2.
Las aplicaciones del PT en dermatología son recientes. La morfogénesis de los folículos pilosos se explica a través de un PT, en el cual la interacción de las vías de señalización celular BMP (proteína morfogenética del hueso), FGF (factor de crecimiento fibroblástico) y WNT (proteína «wingless») dan lugar al condensado epidérmico y dérmico del que se origina la papila3. Los distintos patrones morfológicos de la urticaria crónica espontánea (UCS) se pueden explicar a través de un modelo de activación/inhibición de la histamina4. La morfología y velocidad de los habones de la UCS es distinta a la producida mediante una intradermorreacción de histamina. En la UCS la velocidad de los habones es más lenta, duran más tiempo, y pueden adquirir patrones anulares o arciformes, frente al habón circular de la intradermorreación4. Los patrones morfológicos de la psoriasis (anular, circinada, en rosetas, en grandes placas…) y su evolución también se pueden explicar mediante los PT y la interacción de las citoquinas patogénicas TNF-alfa, IL17 e IL235.
Los modelos matemáticos como los PT pueden explicar el fenotipo de diferentes patologías cutáneas. El papel del dermatólogo resulta fundamental en la búsqueda de las diferentes moléculas, vías de señalización celular y sus interacciones, que permitan explicar estos procesos.
FinanciaciónEste trabajo no ha recibido ningún tipo de financiación.